Использование макромолекул в нанотехнологиях разнообразно, желательно, чтобы участники отметили хотя бы следующие моменты:
-
Создание композитов полимер – наночастицы с различными оптическими и механическими характеристиками,
-
Стабилизация наночастиц (например, в растворе) и их самосборка (как вариант – использование биомолекул ДНК)
-
Использование блоксополимеров для создания суспензий (в качестве поверхностно-активных веществ), мезопористых систем (в качестве «шаблонов»), создания «наношаблонов» при расслаивании систем, содержащих блоксополимеры
-
Применение полимеров для создания «микропечатей» в «мягкой литографии»
-
Использование специальных светочувствительных, электропроводящих и т.д. полимеров для создания микрокомпозитов и гибридных материалов
1. Рассмотрим сначала самое нижнее звено макромолекулы. Найдём величину его растяжения из закона Гука. F = kx, откуда x=F/k. Сила натяжения нижнего звена равна силе тяжести, действующей на нижний грузик массой m: F = mg. Получаем, что нижнее звено растянется на величину x=mg/k.
Второе снизу звено растянется на величину 2x (т.к. общая сила тяжести уже в 2 раза больше), третье – на 3x, четвёртое – на 4x, и так далее. Получается арифметическая прогрессия. Сумма n членов арифметической прогрессии равна Sn(1). В нашей прогрессии и первый член a1, и разность d равны величине x. Поэтому общее изменение длины равно: (2) Sn ≈ 9•10-13 м.
Первое приближённое равенство выполняется потому, что n много больше единицы.
Такое растяжение трудно зафиксировать экспериментально, и более того, оно сравнимо с растяжениями от других факторов (например, теплового движения атомов макромолекулы). Поэтому данный метод измерения неприменим.
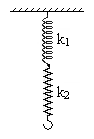
2. Обозначим коэффициент жёсткости одного звена за k0. Чему равен общий коэффициент жёсткости молекулы из n звеньев? Решим вспомогательную задачу. Две пружины с коэффициентами жёсткости k1 и k2 соединены так, как показано на рисунке 1. Чему равен общий коэффициент жёсткости получившейся конструкции?
Представим, что конструкцию растянули некоторой силой F. Так как нижняя пружина находится в равновесии, то на неё со стороны верхней пружины действует сила, тоже равная F (массу пружин не учитываем, как и в предыдущих задачах). Значит, обе пружины растянуты с силой, равной F. Удлинение системы равно сумме удлинений каждой из пружин: x=x1+x2 . Пусть k – коэффициент жёсткости системы. По закону Гука, F=kx=K(x1+x2). Теперь x1 и x2 нужно выразить через F, k1 и k2: , x1=F/k1, x2=F/k2. Эти выражения подставим в предыдущую формулу, F сократится, и можно будет выразить из получившегося равенства k. Получается следующее: (3)
Этот результат можно сообщить и на случай, когда соединены не две, а n пружин: (4)
В нашем случае коэффициенты жёсткости всех «пружин» (звеньев молекулы) одинаковы и равны k0, и всего их n штук. Поэтому имеем: (5)
Мы выразили коэффициент жёсткости одного звена через коэффициент жёсткости всей молекулы, который теперь надо найти.
Максимум амплитуды колебаний молекулы свидетельствует о резонансе: период собственных колебаний молекулы равен периоду звуковой волны. Период собственных колебаний пружинного маятника равен (6). Период звуковой волны равен (7), где υ – скорость звука в воздухе. Приравнивая эти величины и выражая k, имеем: (8). Тогда коэффициент жёсткости одного звена равен (9) ≈ 0,0046 Н/м.
3. Нужно рассмотреть половину цепочки (левую или правую) и записать условие равновесия.
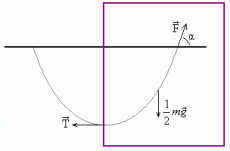
Рассмотрим правую половинку. Векторная сумма всех действующих на неё сил (это три силы, изображённые на рисунке 2) равна нулю: (10).
Спроецируем это векторное равенство на горизонтальную ось: T=F*cos(a), и на вертикальную ось:0,5*mg=F*sin(a). Деля одно уравнение на другое и выражая T, получим ответ: (11)= 2,88•10-18 Н.
4. Каждый грузик в дискретной модели приходится на длину L в непрерывной модели. По определению плотности, имеем: (12).
Коэффициент жёсткости цилиндрического тела с площадью основания S и высотой L связан с модулем упругости материала, из которого оно сделано, следующим образом (это следует из определения модуля упругости): k=ES/L. Отсюда выражаем (13).
5. Чтобы решить последнюю часть задачи, проще всего сделать обратный переход: от непрерывной модели к дискретной. Однако этот переход нельзя сделать однозначно. Например, покопавшись с формулами, вы могли убедиться, что нельзя однозначно определить длину дискретного звена L из параметров непрерывной модели. Как же заменить непрерывную модель дискретной? При этой замене длину структурного звена нужно устремить к нулю (или, что эквивалентно, число структурных звеньев устремить к бесконечности).
Введём сначала модель, в которой длина структурного звена равна L (а число звеньев равно n=Lo/L), а потом устремим L к нулю.
Подобно первой части этой задачи, рассмотрим сначала нижнее звено. Его удлинение равно x0=mg/k. Удлинение каждого звена на d=mg/k больше, чем удлинение предыдущего. Имеем арифметическую прогрессию. Сумма n членов арифметической прогрессии равна (14) .
Видим, что L и S сократились. Поэтому сумма членов арифметической прогрессии при стремлении L к нулю не меняется. Она вообще не зависит от L, хотя число n членов прогрессии и сами эти члены от L зависят. Таким образом, полученная формула является окончательной, и остаётся подставить числа и посчитать.
Вычисления дают: 12,5 см.