«Под микроскопом он открыл, что на блохе
Живет блоху кусающая блошка;
На блошке той блошинка-крошка,
В блошинку же вонзает зуб сердито
Блошиночка, и так ad infinitum»
Д.Свифт.
Нравится ли вам смотреть на ночные молнии или представлять синии всполохи ветвящихся разрядов электрического оружия наноробота, разглядывать морозные узоры на окне или, может, вы любите ловить так непохожие друг на друга снежинки и рассматривать их неповторимую форму? Если да, то вам, несомненно, понравятся и фрактальные структуры!
Фракталами называют бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба. Разветвления трубочек трахей, нейроны, сосудистая система человека, извилины берегов морей и озер, контуры деревьев — это все фракталы. Фракталы находят в местах таких малых, как клеточная мембрана, и таких огромных, как звездные галактики. Можно сказать, что фракталы – это уникальные объекты, порожденные непредсказуемыми движениями хаотического мира!
Термин «фрактал» был введен Б.Мандельбротом в 1975 г.. Согласно Мандельброту, фракталом (от лат. «fractus» - дробный, ломанный, разбитый) называется структура, состоящая из частей, подобных целому. Свойство самоподобия резко отличает фракталы от объектов классической геометрии. Термин самоподобие означает наличие тонкой, повторяющийся структуры, как на самых малых масштабах объекта, так и в макромаштабе.
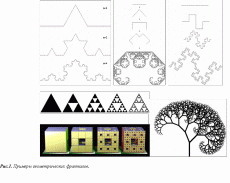
История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса – самые наглядные, потому что в них сразу видно самоподобие. Примерами таких фракталов служат: кривые Коха, Леви, Минковского, треугольник Серпиньского, губка Менгера, дерево Пифагора (Рис.1) и др. С математической точки зрения, фрактал - это, прежде всего, множество с дробной (промежуточной, «не целой») размерностью. В то время как гладкая евклидова линия заполняет в точности одномерное пространство, фрактальная кривая выходит за пределы одномерного пространства, вторгается за границы в двумерное пространство. Таким образом, фрактальная размерность кривой Коха будет находиться между 1 и 2. Это, прежде всего, означает, что у фрактального объекта невозможно точно измерить его длину!
Существует множество классификаций фракталов. Принято различать регулярные и нерегулярные фракталы, из которых первые являются плодом воображения (математическая абстракция), подобным снежинке Коха или треугольнику Серпинского, а вторые - продуктом природы или деятельности человека. Нерегулярные фракталы (рис.2) в отличие от регулярных сохраняют способность к самоподобию в ограниченных пределах, определяемых реальными размерами системы.
Фракталы находят все большее и большее применение в науке и технике. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Можно до бесконечности приводить примеры фрактальных объектов в природе, - это и облака, и хлопья снега, и горы, и вспышка молнии, и наконец, цветная капуста. Фрактал как природный объект - это вечное непрерывное движение, новое становление и развитие.
Кроме того, фракталы находят применение в децентрализованных компьютерных сетях и «фрактальных антеннах». Весьма интересны и перспективны для моделирования различных стохастических (не детерминированных) «случайных» процессов, так называемые «броуновские фракталы». В случае нанотехнологии фракталы тоже играют важную роль, поскольку из-за своей иерархической самоорганизации многие наносистемы обладают нецелочисленной размерностью, то есть являются по своей геометрической, физико-химической или функциональной природе фракталами. Например, ярким примером химических фрактальных систем являются молекулы «дендримеров». Кроме того, принцип фрактальности (самоподобной, скейлинговой структуры) является отражением иерархичности строения системы и поэтому является более общим и универсальным, чем стандартные подходы к описанию строения и свойств наносистем.
Литература
Третьяков Ю.Д. Дендриты, Фракталы и Материалы, Соросовский Образовательный Журнал. 1998. № 11. С. 96-102.
Федер Е. Фракталы.-М.: Мир, 1991. С.254.