В издательстве УРСС вышло в свет репритное издание книги выдающегося отечественного математика, механика, педагога и философа Дмитрия Дмитриевича Мордухай-Болтовского «Геометрия радиолярий».
Предлагаем нашим читателям вступительную статью к этому изданию с послесловием автора статьи, написанным специально для «Нанометра». Данная статья объясняет, почему книга, изданная в 1936 г. и положившая начало развитию в нашей стране новой науки - математической биологии, сегодня вызовет интерес у представителей разных отраслей знания, в частности, науки о наноматериалах и нанотехнологиях.
Идеи не умирают. Они мигрируют в другие области
жизни, они рассредоточиваются по частям, они
оборачиваются к нам своей изнанкой — но и в
другой точке пространства, но и в отдельной
части, но и в изнанке, наконец,- легко узнаётся всё
то же вещество, та же плоть, та же
бессмертная душа первоначального прозрения.
Ю. Карабчиевский
Дмитрий Дмитриевич Мордухай-Болтовской (1876-1952) – выдающийся российский математик, механик, педагог, автор русского перевода "Начал" Евклида (два издания, 1948-1950 гг.) и «Математических рукописей» Ньютона и подробных комментариев к ним, а также оригинальный и независимый философ (по всей вероятности, один из последних представителей блестящей плеяды русских философов-идеалистов). Его научная, педагогическая и общественная деятельность продолжалась более пятидесяти лет, не самых лёгких в российской истории, включавших революции, войны, гибель близких, эвакуацию и переезды из города в город, сталинский террор и идеологический диктат, бедность материального существования.
Научные интересы Мордухай-Болтовского были необычайно широки и включали такие разные области математики, как интегрирование дифференциальных уравнений в конечном виде, теорию трансцендентных чисел и гипертрансцендентных функций (знакомство с этими работами Мордухая-Болтовского, по выражению А.О.Гельфонда, должно быть "обязательно для всех интересующихся этими вопросами"), теорию алгебраических кривых, топологию, дифференциальную геометрию, в том числе в пространстве Лобачевского, теорию геометрических построений на плоскости Евклида, а также в пространстве Лобачевского и на сфере. Широта математических интересов Мордухай-Болтовского не помешала ему в каждой из областей исследования получить значительные результаты.
Более 50 различных курсов прочитал Дмитрий Дмитриевич в высших учебных заведениях (от Варшавского Политехнического института и Варшавского Императорского университета до Ростовского Государственного университета). Мордухай-Болтовской оказал глубокое влияние на развитие российской математики и науки в целом и как создатель математической школы, многие представители которой основали собственные научные школы и новые направления науки. Назову лишь несколько имён выдающихся ученых – учеников Мордухай-Болтовского. Математик и кибернетик академик В. М. Глушков по праву считается создателем первых образцов отечественной вычислительной техники. Б.М. Щиголев основал кафедру вычислительной математики МГУ и был её первым заведующим. Один из основателей советской историко-математической школы М.Я. Выгодский был соавтором своего учителя по работе над изданием Евклида. Он также - автор предисловия и комментариев к трехтомному "Интегральному исчислению" Леонарда Эйлера. Среди учеников Мордухай-Болтовского - выдающиеся математики А.Ф.Бермант, Б.Я.Левин, Н.В.Ефимов, известный математик и астроном, член-корреспондент АН СССР М.Ф.Субботин, и, как ни странно … А.И. Солженицын. Бывший студент физико-математического факультета Ростовского университета вывел своего давнего профессора на страницы двух романов "Март семнадцатого" и "В круге первом"*.
В книге «Геометрия радиолярий», вышедшей в свет в 1936 году в издательстве Ростовского университета, репринтное издание которой издательство УРСС предлагает современному читателю, Д. Д. Мордухай-Болтовской выступает как пионер абсолютно новой по тем временам науки – математической биологии. Сегодня эта наука переживает свой звездный час, и только поэтому книге обеспечен читательский интерес.
Я же хочу взглянуть на это классическое произведение с несколько необычной точки зрения и обратить внимание на кажущуюся парадоксальной (но только - на первый взгляд) связь этой работы Д.Д. Мордухай-Болтовского с происходящей в наши дни нанотехнологической революцией, а конкретно, с исследованием и разработкой наноматериалов на основе фуллеренов, молекул чистого углерода, открытых в конце XX века. Не сомневаюсь, что среди читателей «Геометрии радиолярий» будут и те, кто профессионально занимается исследованием фуллеренов, и те, кто только начинает изучать науку о фуллеренах, и конечно, все те, кто интересуется историей этой науки. Таких читателей немало и в нашей стране и за рубежом (последнее указывает на весьма возможный интерес к изданию переводов книги на другие языки).
Чтобы не быть голословным, мне придется объяснить, что такое фуллерены, какова их структура, и что общего в ней со строением радиолярий.
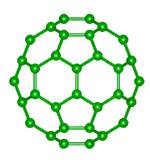
Рис. 1. Молекула С60
В 1985 г. молекула С60, состоящая из 60 атомов углерода, была экспериментально открыта английским астрохимиком Г. Крото и американскими физико-химиками Р. Смолли и Р. Кёрлом. Исследователи предположили, что атомы углерода в этой молекуле находятся в вершинах усеченного икосаэдра - многогранника, напоминающего по форме футбольный мяч (рис. 1, а, б). Этот многогранник имеет 32 грани (20 правильных шестиугольников и 12 правильных пятиугольников) и 60 вершин (атомов углерода). Новой молекуле было присвоено имя бакминстерфуллерен, в честь американского архитектора Р. Бакминстера Фуллера, автора концепции геодезических куполов – зданий-многогранников.
В 1996 г. Крото, Кёрлу и Смолли за экспериментальное открытие фуллеренов была присуждена Нобелевская премия по химии.
Вслед за С60 были открыты и другие фуллерены – семейство замкнутых многогранных молекул чистого углерода, имеющих только пяти- и шестиугольные грани.
Исследования методов получения фуллеренов привели впоследствии к другому замечательному достижению – открытию углеродных нанотрубок.
Открытие С60 явилось своеобразным волшебным «золотым ключиком» в новый мир нанометровых структур. К настоящему времени обнаружено большое количество фуллереноподобных кластеров из чистого углерода (а также из других элементов и неорганических соединений) с фантастическим (в прямом смысле этого слова!) разнообразием структуры и свойств. Это открытие, безусловно, было одним из основных стимуляторов сегодняшней нанотехнологической революции, послужив основой для разработки новых наноматериалов и технологий, которые в третьем тысячелетии найдут применение в наноэлектронике, солнечной энергетике и других отраслях техники.
Решающую роль в построении гипотезы о структуре фуллеренов сыграло применение теоремы, сформулированной и доказанной в XIII веке великим математиком Леонардом Эйлером (1707–1783). В двух статьях, опубликованных в “Записках Петербургской Академии Наук” в 1758 г. – “Элементы учения о телах” [1] и “Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями” [2], Эйлер сформулировал и доказал теорему о соотношении между числом вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В – Р + Г = 2.
Из знаменитой теоремы вытекают некоторые важные для рассматриваемой проблемы следствия. В частности, тот факт, что не существует выпуклого многогранника, у которого все грани были бы шестиугольниками. Это в свою очередь означает, что нельзя сконструировать молекулу углерода (так же, как и любую другую молекулу) со структурой многогранника только посредством шестиугольников. Поэтому в молекуле С60 кроме шестиугольных имеются и пятиугольные грани. Последние необходимы для искривления плоской (шестиугольной) графитовой структуры и превращения ее в замкнутую оболочку. Более того, соотношение Эйлера "требует" наличия 12 (не больше и не меньше!) пятиугольных граней в любой из таких молекул. А вот число шестиугольных граней может варьироваться, и при этом число вершин многогранника (атомов углерода) всегда остается четным. По такой логике наименьшая молекула фуллерена, С20, состоит только из 12 пятиугольников. Следующий фуллерен – С24, затем С26, С28, .., С60, .., С70, С72, … и т. д. Применение соотношения Эйлера позволяет также объяснить уникальность и особую стабильность С60 в сравнении с другими фуллеренами.
Структуры, подобные фуллеренам, использует и живая природа. Фуллереноподобную структуру имеют многие вирусы и бактериофаги, и конечно же – радиолярии, морские одноклеточные микроорганизмы (Radiolaria) (рис. 2). В любом случае – будь то вирус, микроорганизм или даже творение человеческих рук, например, архитектурные сооружения, соотношение Эйлера требует в такой структуре наряду с произвольным числом шестиугольных граней наличия 12 пятиугольников.
Любопытно, что приведенный выше вывод был заимствован исследователями фуллеренов из анализа формы и структуры скелета радиолярий, описанного в книге “Рост и форма” выдающимся шотландским математиком и биологом Д’Aрси Томпсоном (1860-1948) [3].
Рис. 2. Рисунки радиолярий из книги Э. Геккеля «Челленджерский отчёт». Воспроизводится по книге Д’Aрси Томпсона “Рост и форма” [3].
Книга “Рост и форма» – шедевр научной литературы, автор которого по словам Генриха Вейля «сочетал в себе глубокое знание геометрии, физики и биологии с гуманитарной культурой и необычайно оригинальным даром проникновения в существо научных проблем». Именно благодаря этому редкому сочетанию качеств автора, книга “Рост и форма”, в которой впервые в столь обширной и подробной манере суммированы результаты применения математических и физических методов к исследованию объектов живой природы, стала научным бестселлером, настольной книгой многих поколений читателей. Изданная в 1917 году издательством Кембриджского университета (Cambridge University Press), эта книга была пять раз переиздана только этим издательством: в 1942, 1952, 1959, 1963 и 1992 годах. Последние четыре издания осуществлены уже после смерти автора. Безусловно, эта книга будет переиздаваться и в XXI веке. Надеюсь, что среди этих изданий будет и первый русский перевод книги.
Радиолярии – планктонные организмы размером от 40 мкм до 1 мм. Это поистине уникальные создания (хотя какие из созданий живой природы не уникальны?!). Они сами строят свой скелет из солей кремния, поглощаемых ими же из морской воды. Из повседневной жизни каждый из нас знает, что, когда делаешь что-либо самостоятельно, для себя и на свои средства, то, скорее всего, постараешься выполнить это самым эффективным и экономным способом. Жизнь радиолярий протекает в состоянии парения в морской воде, поэтому в строении их скелета должны сочетаться легкость и прочность, что и обеспечивается фуллереноподобной структурой. Именно такое сочетание требований привело Бакминстера Фуллера к концепции геодезической структуры его зданий-куполов.
То, что первооткрыватели фуллеренов использовали подход, изложенный в книге Д’Aрси Томпсона, не вызывает сомнений. А вот в том, что Д’Aрси Томпсон выполнил этот анализ первым, для меня с некоторого времени не столь очевидно. Или не только он был первым. В 2004 году, работая над книгой «Фуллерены, углеродные нанотрубки и нанокластеры: родословная форм и идей», я наткнулся в статье Юрия Войтеховского [4] на ссылку на книгу Д. Д. Мордухай-Болтовского «Геометрия радиолярий»
Имя Мордухай-Болтовского мне тогда ни о чём не говорило, а найти его работу представлялось абсолютно невозможным. А хотелось очень!
Долгий поиск в Интернете вывел меня на сайт [5] исследователя творчества Д. Д. Мордухай-Болтовского, собирателя и хранителя его архива Вячеслава Пыркова из Ростова-на-Дону. Так завязалось наше виртуальное знакомство с Вячеславом, перешедшее, наконец, в реальное в 2007 году в Санкт-Петербурге на конференции, посвящённой трёхсотлетию Леонарда Эйлера.
Благодаря материалам, присланным мне Вячеславом Пырковым и размещённым на его сайте, я многое узнал о Мордухай-Болтовском, прочитал «Геометрию радиолярий», другие его работы, письма и фрагменты неопубликованных рукописей, а, главное, был, без всякого преувеличения, просто поражён масштабом личности этого Учёного и Мыслителя.
«Геометрия радиолярий» поражает тщательностью проработки проблемы и мощью математического арсенала автора. Для анализа форм радиолярий автор применяет теорию многогранников, которой занимался в течение всей долгой творческой жизни, элементы вариационного исчисления, топологию, дифференциальные уравнения.
Первая глава второй части книги, названная «Ситуационная геометрия радиолярий», посвящена анализу их структуры с помощью теоремы Эйлера и содержит в себе практически все соображения, приведённые нами выше. Параграф 5 этой главы называется «Теорема Эйлера и непосредственные следствия из неё». Следующие два параграфа распространяют эти следствия на случаи правильных, полуправильных и неправильных тел.
Мордухай-Болтовской мог познакомиться с книгой Томпсона, например, через А.А. Любищева**, с которым он состоял в интенсивной переписке. Но если это и произошло, то, скорее всего, уже после написания "Геометрии радиолярий». Во всяком случае, скурпулёзно перечисляя источники, Мордухай-Болтовской не упоминает книгу Томпсона ни в предисловии к своей книге, ни в материалах, имеющихся в архиве Пыркова. Вот, например отрывок из присланного мне последним "Отчета о работе летом 1929 г. на пособие от Ассоциации исследовательских институтов" (сохранена орфография Мордухай-Болтовского):
"Для основной своей темы - геометрия радиолярий - я преимущественно использовал капитальный труд Геккеля (Report of the Scient. Results of the voyage of Challenger, XIII том). Это необыкновенно роскошное издание с изображением огромного числа видов радиолярий и с подробным их описанием. Я имел терпение снять на кальку более сотни снимков и переписать в тетрадь текст. За этим трудом следует знаменитая работа Геккеля «Die Radiolarien. Berlin. 1862», которая, конечно уже в виду её устарелости даёт меньше материала. Были и здесь скалькированы рисунки, но они представляли большей частью лишь повторение того, что я нашел в первой книге. Упомяну Acantarien Поповского и монографию Шевякова, давшие тоже снимки и выписки из текста. Наконец, работы Hertwig-a, Muller-a, Brandt-a. Удалось мне также изучить и интересную для геометра «Протоморфологию» Геккеля. Из учебников по зоологии, мной просмотренных, укажу на книгу «Delage et Nerouerd. Traité de Zoologie
concrète t. I. 1896», где очень подробно говорится о радиоляриях. Что касается до работ, относящихся к многогранникам, то удалось познакомиться с классическим мемуаром Gordan, «Морфологией полиэдра» Eberhardt, а также со статьями Möbius в полном собрании его трудов. Проблемы о максимумах и минимумах, относящихся к многогранникам, столь важные в предпринятой биологико-геометрической работе, я изучал … в работах Штейнера, Линделёфа и других. По кристаллографии… я … ознакомился с «Кристаллографией» Шенфлиса, где применяется теория групп и учебником Soret и Aroth".
Только Геккеля Мордухай-Болтовской упоминает и в самой «Геометрии радиолярий» как своего предшественника: «Приступая к геометрическим исследованиям форм организмов, я должен отметить, что геометрическая точка зрения здесь не является совершенно новой. Геккель в своей «Протоморфологии» классифицирует органические формы, как кристаллы, на основании элементов симметрии».
И ни слова о Томпсоне.
Я практически уверен, что Д’Aрси Томпсон читал книгу Д.Д. Мордухай-Болтовского. Такой вывод я сделал после знакомства с присланным мне В. Пырковым отрывком из неизданной рукописи "Автобиографии профессора Д.Д. Мордухай-Болтовского от 7 февраля 1946 года", где учёный пишет: "Из математическо-биологических работ (часть которых погибла) удалось напечатать только о крылатках и летучках растений и соответствующих им аппаратах низших водных животных и геометрию радиолярий. С последней работой некоторые заграничные биологи ознакомились благодаря переводам, а д'Арси-Томпсон в Шотландии, знал в некоторой мере русский язык. От последнего получил очень хороший отзыв". Этот отзыв В. Пыркову пока найти не удалось. Дело в том, что во время войны сгорела квартира и абсолютно все имущество семьи Мордухай-Болтовского, включая богатую переписку с Вейлем, Риттом, Адамаром и многими другими зарубежными учёными.
Два вопроса представляются важными в контексте нашей истории: когда была написана Томпсоном глава о радиоляриях и теореме Эйлера, и как это соотносится со временем знакомства шотландского учёного с работой Мордухай-Болтовского?
Не вызывает сомнения, что подавляющее большинство современных читателей, и в их числе – упомянутые выше исследователи фуллеренов, познакомились с книгой Томпсона по посмертным (послевоенным) изданиям. В предисловии к изданию 1963 года [3] автор пишет, что ко второму изданию (1942) - и только к нему - книга была существенно дополнена. Совсем недавно, в библиотеке Гарвардского университета мне удалось разыскать первое издание книги Томпсона 1917 года и ответить на первый вопрос: интересующий нас анализ в данном издании отсутствует, то есть он был добавлен Томпсоном в книгу только в 1942 г., а значит, был впервые выполнен и опубликован Мордухай-Болтовским в 1936 г.
Получить ответ на второй вопрос, вероятно, совсем непросто. Вполне возможно, и этот вариант представляется мне наиболее правдоподобным, что оба исследователя пришли к похожим результатам независимо друг от друга. Как бы то ни было, этими результатами мы пользуемся сегодня при анализе фуллереноподобных структур.
С другой стороны, изучение структуры и свойств фуллеренов вызвало в последние десятилетия совершенно необычайный исследовательский бум. Это уже позволило накопить новые знания, которые теперь, на современном витке спирали научного познания применяются для более глубокого понимания строения радиолярий, вирусов, бактериофагов и других фуллерено-подобных объектов живой природы. Именно о них писал уже упоминавшийся Эрнст Геккель: «Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы».
И прежде, чем пригласить читателей взглянуть на эти «удивительные создания» глазами выдающегося математика Д. Д. Мордухай-Болтовского, необходимо отметить, что настоящее издание было бы невозможным без постоянной помощи В. Е. Пыркова, а также доброжелательной поддержки идеи переиздания книги со стороны Эмилии Дмитриевны Мордухай-Болтовской и Людмилы Филаретовны Болтовской.
Послесловие автора статьи.
21 мая 2012 г., то есть уже после выхода книги в свет, я получил письмо от В.Е. Пыркова с очень важным для нашей истории известием. В московском Архиве РАН исследователю удалось найти письмо Д.Д. Мордухай-Болтовского к Владимиру Ивановичу Вернадскому, датированное 9 июня 1939 г.. В этом письме математик уведомляет Вернадского, что только что ознакомился с книгой Д’Aрси Томпсона “Рост и форма” и благодарит Владимира Ивановича за помощь в получении книги. Эта находка документально подтверждает одно из двух высказанных мной предположений: Д.Д. Мордухай-Болтовской прочитал книгу Томпсона после написания и публикации своей «Геометрии радиолярий».
Литература.
1. Euler, L. Elementa doctrinae solidorum // Novi commentarii academie Petropolitanae 1758. V. 4. P. 109–140.
2. Euler, L. Demonstratio nonnullarum insignium proprietatum, quibus solida hedris planis inclusa sunt praedita // Novi commentarii academie Petropolitanae. 1758. V. 4. P. 140–160.
3. Thompson, D’A. W. On growth and form. Cambridge University Press, 1963.
4. Войцеховский, Ю. Л.. Природа, 2004, №8, 8-18.
5. http://pyrkovve.narod.ru/index.html
Сведения об авторе статьи
Евгений Адольфович Кац – профессор университета им. Бен-Гуриона в Негеве (Израиль), автор ~200 научных работ по широкому спектру физических и материаловедческих проблем солнечной энергетики и, в частности фотоэлектрическим свойствам наноматериалов, и ряда научно-популярных статей, посвященных фуллереноподобным структурам в углеродных наноматериалах, живых организмах и архитектуре, а также книги «ФУЛЛЕРЕНЫ, УГЛЕРОДНЫЕ НАНОТРУБКИ И НАНОКЛАСТЕРЫ: РОДОСЛОВНАЯ ФОРМ И ИДЕЙ», М.: УРСС, 2008 (2-е изд, 2009).
* В "В круге первом" – под именем Дмитрия Дмитриевича Горяинова-Шаховского.
** Александр Александрович Любищев (1890-1972) – один из крупнейших русских мыслителей XX века, выдающийся энтомолог, философ, автор классических работ по теории систематики, сравнительной анатомии и эволюционному учению, ярый сторонник применения математических методов в биологии.