В сканирующей зондовой микроскопии, и в первую очередь в сканирующей туннельной микроскопии, нам не редко удается работать с органическими веществами, формирующими высоко упорядоченные тонкие пленки или кристаллические структуры.
Такие объекты прекрасно подходят для того, чтобы поставить перед собой амбициозную задачу: получить картинки поверхности с эффектным молекулярным разрешением. В ряде случаев такие изображения допускают построение пространственной модели элементарной ячейки пленки или кристалла. Общая проблема таких изображений – их зашумленность. Для того чтобы улучшить их качество используются методы корреляционного анализа. Здесь речь пойдет о том, какой эффект дают корреляционные фильтры для улучшения изображений периодических структур, и как они реализованы в программе ФемтоСкан Онлайн.
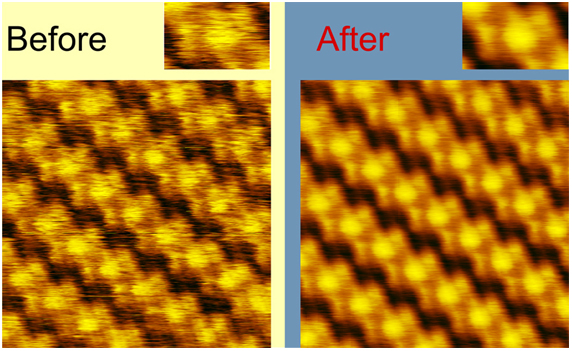
Рисунок 1. Улучшение изображения периодической структуры при помощи корреляционного фильтра.
В начале немного формул и другой серьезной информации, а в конце будет еще два примера того, насколько можно улучшить изображения при помощи корреляционного анализа.
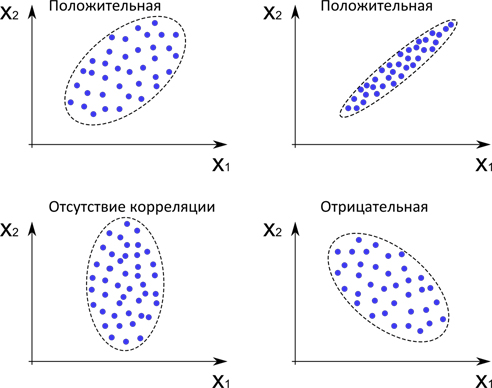
Итак, корреляцией называется статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Например, мы можем измерять рост и вес разных людей и каждое измерение представлять точкой в двухмерном пространстве. Несмотря на то, что величины носят случайный характер, некоторая зависимость между ними будет наблюдаться, это пример положительной корреляции.
Рисунок 2. Две величины, связанные разными статистическими закономерностями.
Взаимосвязь между величинами необходимо охарактеризовать численно, например, для того, чтобы различать два случая, показанных в верхней части рисунка 2. Математической мерой корреляции двух случайных величин служит коэффициент корреляции. Для массива из n точек (x1i, y1i) его можно определить по-разному, например следующим образом:
Корреляционной функцией называется функция времени или пространственных координат, которая задает изменение корреляции в системах со случайными процессами, во времени или в пространстве, соответственно. И в случае обработки изображений оперируют именно двумерными корреляционными функциями:
Теперь у нас есть два изображения, первое изображение z(x,y), а второе – t(i,j) – назовем шаблоном. Обычно шаблон должен быть меньше размером, чем исследуемое изображение, ширину шаблона обозначим через w, длину через l. Значение функции корреляции изображения с шаблоном в точке (x,y) исходного изображения определяется по формуле:
Это выражение еще нужно нормировать, но остановимся на достигнутом, чтобы не перегружать повествование формулами. Луше посмотрим на пример функции корреляции, а точнее автокорреляции изображения калибровочной решетки. Автокорреляция представляет собой статистическую взаимосвязь между случайными величинами из одного ряда, взятыми со сдвигом, например, со сдвигом по времени или по пространству:
Рисунок 3. Изображение калибровочной решетки и его автокорреляционная функция.
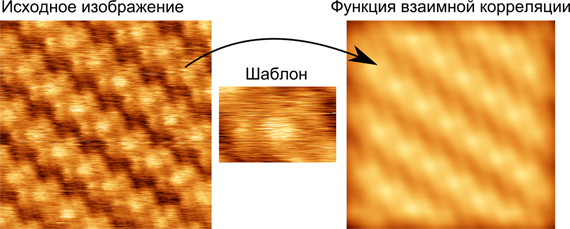
На рис. 2 хорошо видны 6 локальных максимумов корреляции. Алгоритм новой функции программы ФемтоСкан Онлайн Найти структурный элемент основан как раз на поиске локальных максимумов взаимной корреляции изображения периодической структуры и шаблона - небольшого выделенного фрагмента того же изображения, на котором лучше всего идентифицируется одна или несколько элементарных ячеек периодической структуры.
Рисунок 4. Взаимная корреляция изображения и выделенного из него фрагмента - шаблона.
Итак, когда найдены и отобраны локальные максимумы взаимной корреляции между выбранным шаблоном и исходным изображением, дальше происходит усреднением данных в коррелирующих областях изображения. Последовательность работы с данной функцией подробно изложена в ее описании. При правильной настройке параметров Вы сможете добиться построения улучшенного изображения целиком, его фрагмента нужного размера или изображения одного усредненного элементарного элемента структуры. Ниже приведены два примера применения корреляционного фильтра, которые, как мне кажется, говорят сами за себя.
Рисунок 5. Изображение муара на графите, полученное в СТМ и улучшенное при помощи функции Найти структурный элемент в программе ФемтоСкан Онлайн.
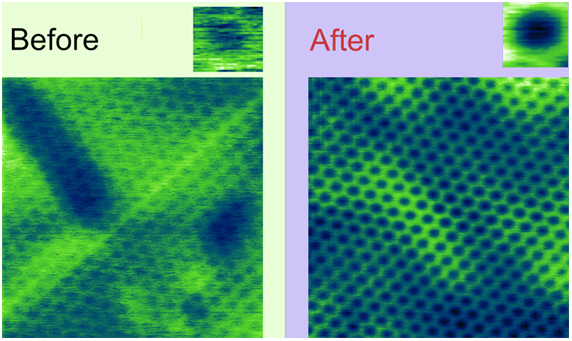
Рисунок 6. Изображение пленки додециламина на поверхности графита, полученное в СТМ и улучшенное при помощи функции Найти структурный элемент в программе ФемтоСкан Онлайн.
Как видите, применение корреляционных фильтров дает не только красивые иллюстрации для статей и постеров, но также позволяет более точно проанализировать структуру исследуемой поверхности. Например, на рис. 6 после обработки стало хорошо видно, что на изображение пленки додециламина накладывается переодически повторяющийся рельеф муара графитовой подложки.
Напоследок хочу выразить благодарность Евгению Дубровину, чьи картинки я использовала для демонстрации возможностей корреляционного фильтра. Спасибо!
Если у Вас есть подобные изображения, нам будет интересно опробовать этот новый метод обработки на них - ждем картинок!

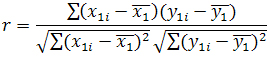
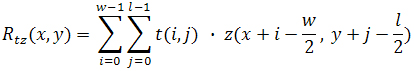




 Идея хорошая, спасибо за инфу.
Идея хорошая, спасибо за инфу.